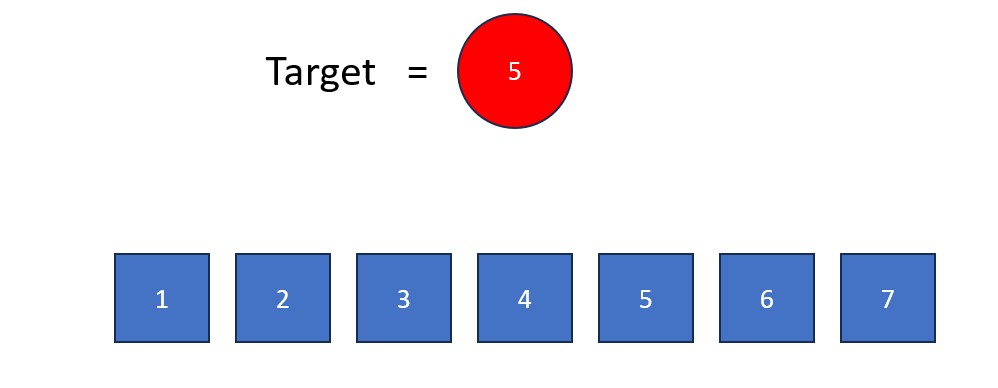
Procedure:
- Make sure the list is sorted in a defined order (ex: ascending or descending).
- Find the median (middle) element of the list. If the list has an even size, use the lesser of the two middle elements.
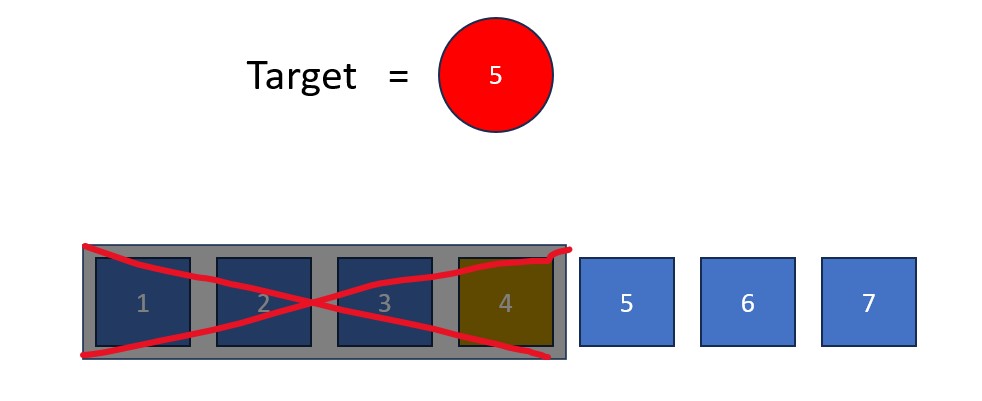
- Compare the median element to the target. If the median > target, eliminate all values to the right of the median (including the median). If the target > median, eliminate all values to the left of the median (including the median).
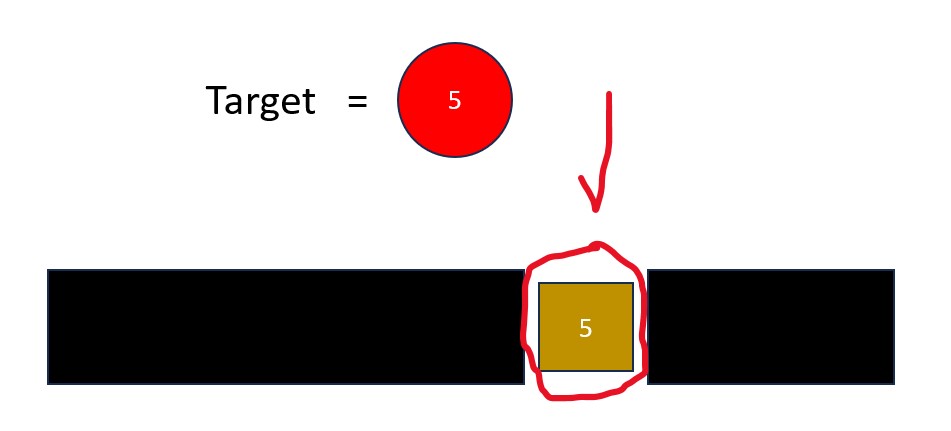
- Repeat steps 2 and 3 until the target value is found as the median or until you run out of values in the list.
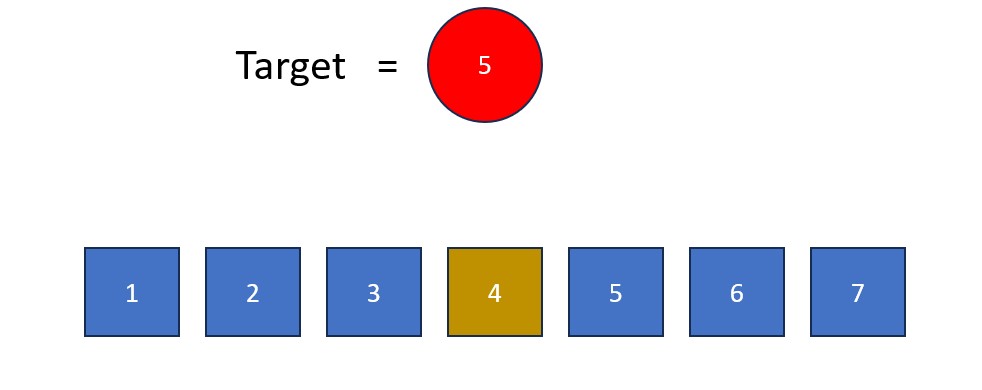

Fun Fact: Binary search is much more efficient than linear search. In a list of 10,000 elements of sorted data, a binary search would take no more than 14 executions to find any piece of data in the list. A linear search could take up to 10,000.