No Code Data Structures

Definition: A binary tree is a data structure in which each node (piece of data) has 0, 1, or 2 other nodes that it is pointing towards in a tree-like structure (see above). A binary heap is a specific type of binary tree in which certain elements are filtered towards the top of the structure. There are two main types of binary heaps:

Real Life Example: To envision a typical binary tree/heap (min heap for this example), think of a reverse family tree in terms of age. You are the youngest in the family and therefore are at the top of the tree. You were born from your two parents, who will be the two nodes that your node points towards. After this each of your parents will point towards their parents and so on. In summary, any given node is smaller than all nodes directly under it (you can't be older than your own parents or grandparents!) making this a min heap.

Basic Properties (See operations section below for applications):

Node: An individual piece of data in a tree. An example is the blue circle with a 15 in it in the picture above.

Root Node: The top node in a tree where all other nodes diverge from. 50 is the root node in the max heap above.

Parent/Child Node: A parent node has at least one node connected directly below it. A child node is a node directly below a parent. In the max heap above, 35 is a child node to 50 but also a parent with child nodes 22 and 9.
Edge: An arrow that connects a parent node to its child node(s).

Leaf Node: Any nodes that have no child nodes. 8 is a leaf node in the max heap above.

Subtree: A smaller tree within the initial binary tree/heap that starts from a parent node besides the root node.

Height: The number of direct edges from the root node to any node given. The height of 8 in the max heap above is 2.

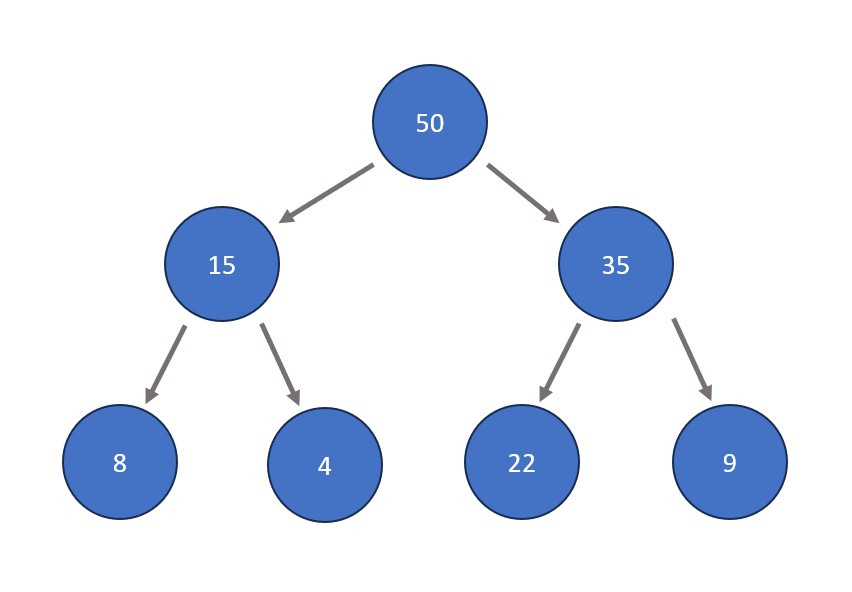
Basic Max Heap Operations:

Note: Min heaps have the same exact procedures as below but checking for nodes being less than those below them rather than greater.

Inserting a node. This is done by first entering the node directly to the right of the right-most node on the bottom level (if the bottom level is full, insert it as the left child node of the left-most node of the bottom level). The node is then shifted directly upwards as many times as needed so that max heap properties are satisfied, meaning that all nodes are greater than all those stemming from below them. This means that if big enough, a value could be swapped all the way up to become the root node.

Removing a node. In a heap structure, this is typically done to the root node in order to remove the absolute extreme of the tree data set. The process involves swapping the node to be removed with the right-most node at the bottom level of the tree. After this swap, the node to be removed (now in a leaf node position) is removed. The node that was swapped is shifted directly downwards as many times as needed so that max heap properties are satisfied, meaning that all nodes are greater than all those stemming from below them.

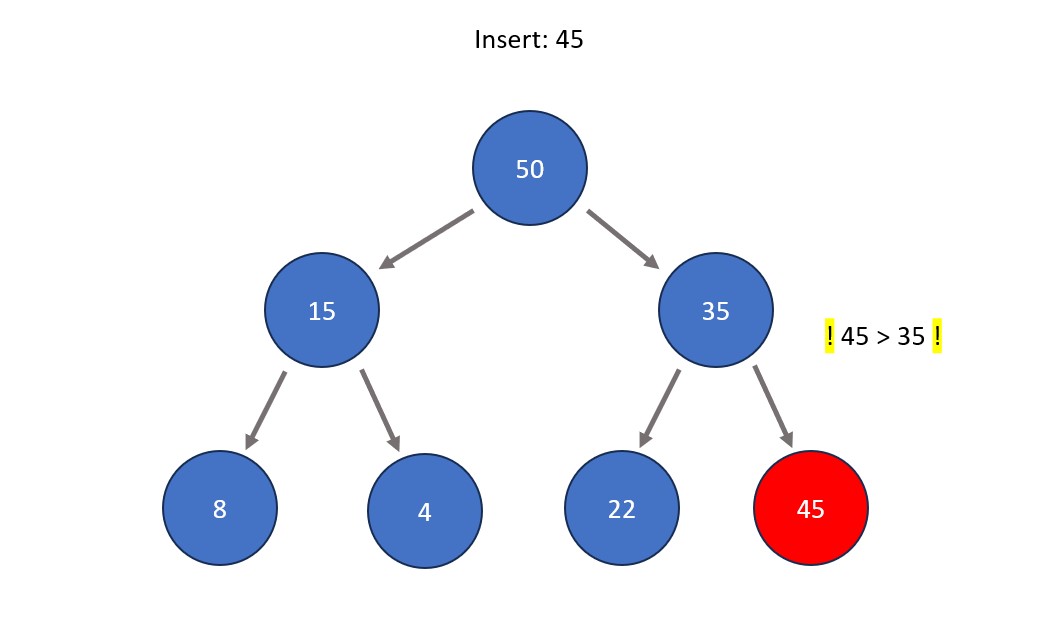
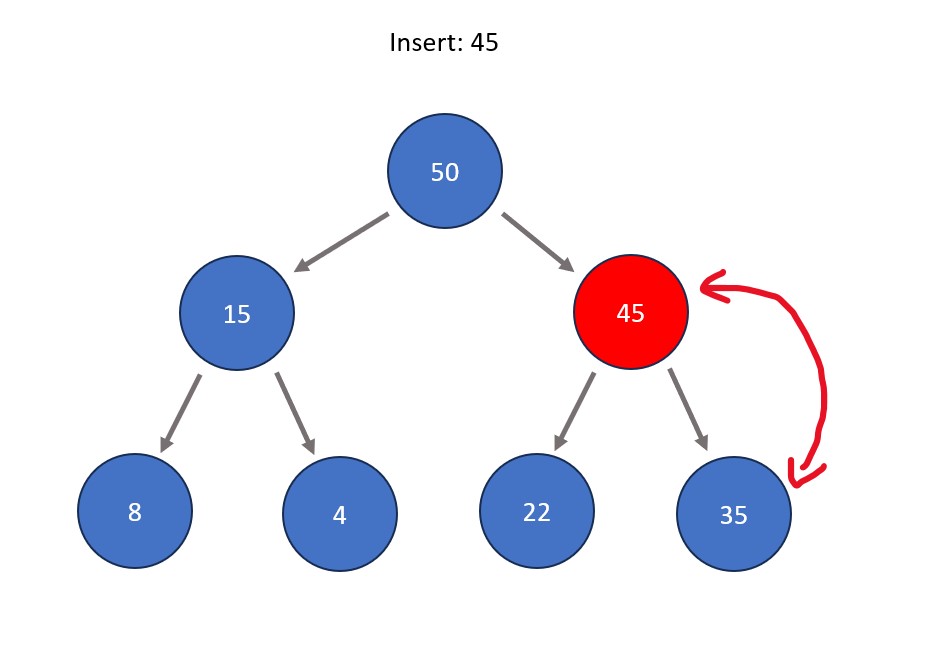
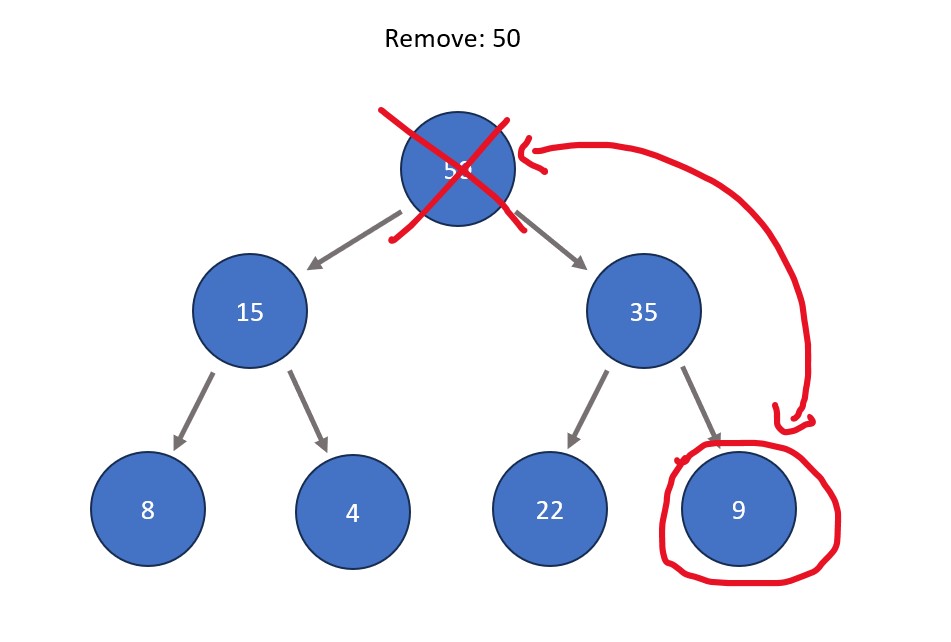
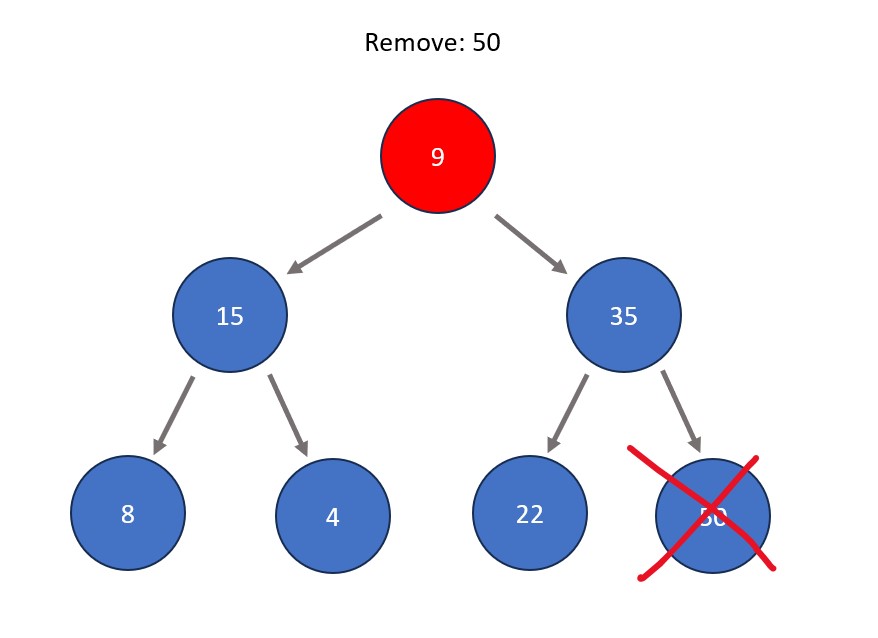
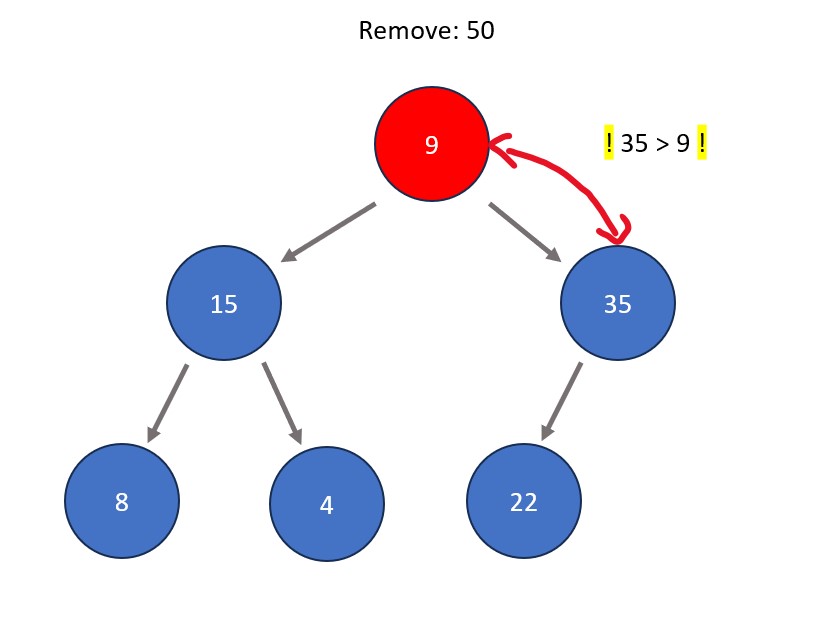
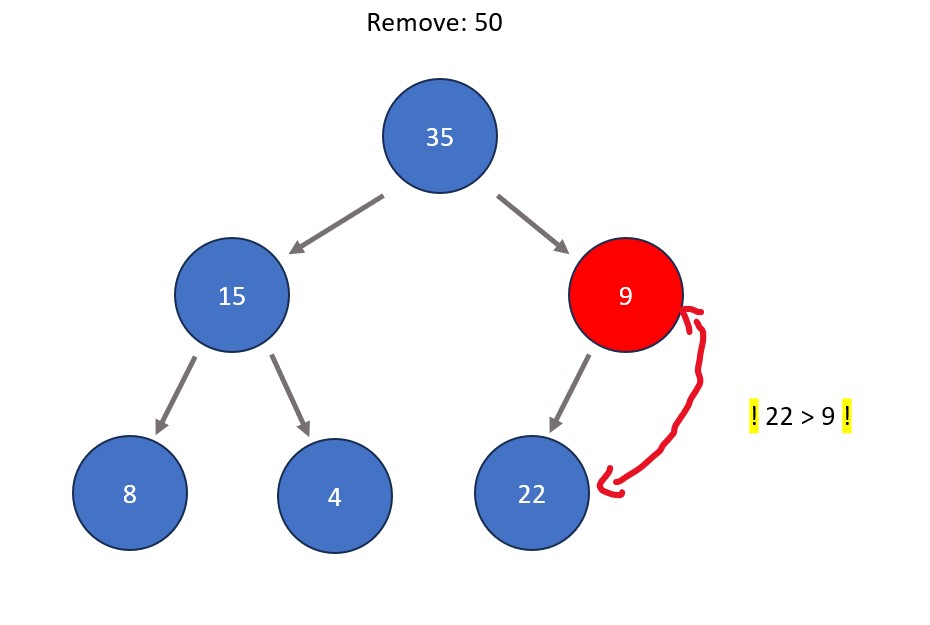
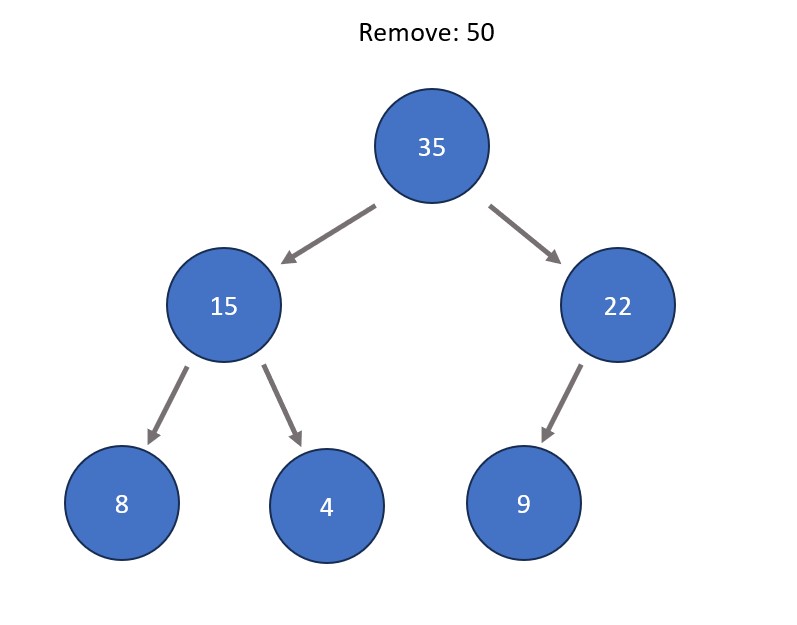
Fun Fact: Repeated deletion of the root node in a heap is the basis a sorting algorithm called heap sort. The idea is that the most extreme element always rises to the top, therefore each time an element is removed from the heap it becomes sorted in comparison to the rest of the removed elements.

Commonly Used In:

System memory management.
Statistical operations.
Implementing other data structures like priority queues and binary search trees.

Other Similar Data Structures:

Treap: A binary tree that contains two values per node: a key that reflects BST
Splay Tree: A type of self-adjusting BST where recently accessed nodes are moved upwards to reduce search times.

Skip List: A sorted, multi-layered linked list used for efficient search, insertion, and deletion of elements. It works by allowing "skips" to speed up searching for elements by jumping over certain irrelevant nodes that waste steps.

Priority Queue: A queue that assigns an intentional priority value to each item upon insertion. When a dequeue occurs, the item with the lowest priority value is deleted rather than the front. If two items are tied for lowest priority value, the one closest to the front is deleted. Heaps are often used to implement priority queues.

Binary Tree/Heap