No Code Data Structures

Definition: Modified depth-first searches that are used to explore and process all nodes in a binary tree. The order the nodes are reached in is the same for all three types, the only difference is when the nodes are processed. See below for an explanation.

Procedures for Pre/In/Post-Order Traversals:

Traversed Binary Tree

Below is the order that preorder, inorder, and postorder traversals all follow when visiting nodes in binary trees (depth-first). As mentioned above, the only difference between the three traversals is when the node is processed. There are no repeats in these traversals, meaning that every node can only be processed once.

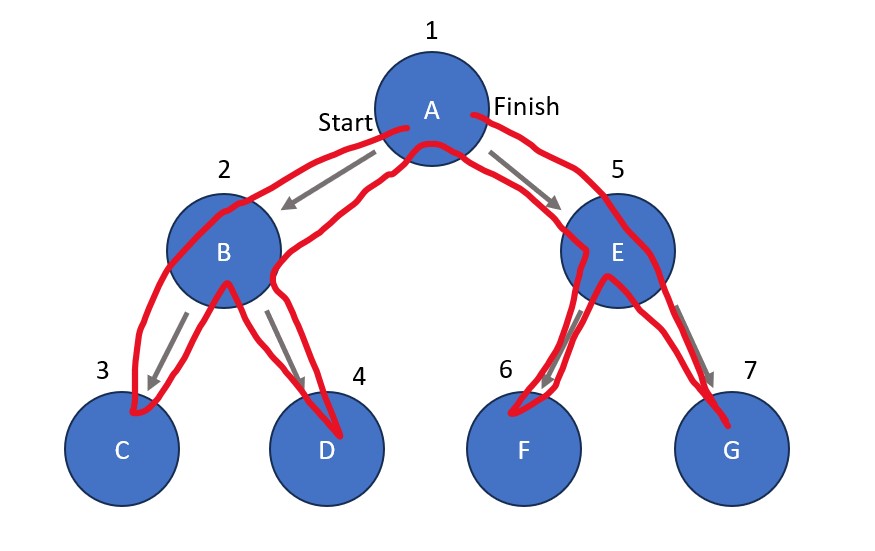
Preorder Traversal: Nodes are processed the second they are reached.

Preorder processing order: A B C D E F G

Inorder Traversal: Nodes are processed after their entire left subtree (anything connected to the bottom left of the node and beyond) is explored. If the node doesn't have a left subtree, it is processed automatically.

Inorder processing order: C B D A F E G

Postorder Traversal: Nodes are processed after their entire left AND right subtrees (anything connected below the node and beyond) is explored. If the node doesn't have a right subtree, it is processed automatically once the left subtree has been explored completely.

Postorder processing order: C D B F G E A

Fun Fact: An inorder traversal of a binary search tree always results in elements being sorted in ascending order.